Logs and Inverses

A major concept that I understood was that a logarithm is the inverse of an exponential function, for example the function 2^x =8 To find the value of x you would need to do the inverse of an exponential function to find the value of the exponent(x). It is basically the same thing as when you are trying to find the value x in the equation x+2=5, To get x by itself you would do the inverse of adding 2 which is subtracting. Now, back to logs in trying to solve the equation 2^x=8 you would take the inverse which is the log base 2 (2^x)=log base 2(8). You would then get x =log base 2 (8),you can simply this more by knowing that 8 is the same thing as 2^3 which would make it log base 2 (2^3) which would make it 3.



Another major concept I understood was the rules of exponents and logarithms for example in logs- log (XY)=log (X) + log (y) , log (X^5)=5log(x), log (X/Y)=log (X)-log(Y). these rules allow you to write and manipulate logs in many different forms. For example you can manipulate log (10) into log (5)+log (2)=log (5x2)=log (10). These rules are very helpful when trying to find a value in an exponential equation or in a logarithm.



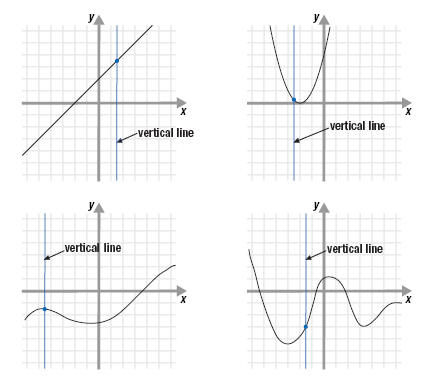
A very important concept that I understood about inverses and functions is that f(f^-1(X))=x and f^-1(f(x))=x. This is very helpful in checking whether or not an inverse function is the inverse of a function. I also understood that a function has to pass the vertical line test which states that if a vertical line was passed through a graphed function it should only intersect the function at one point as seen in the image.
The domain of a function would be what the possible x-values for x can be when inserting into a function or graphically. The domain will give you a boundary about what the inputs(x) can be. The range of a function is the possible y-values of a function meaning a boundary of what the outputs(y) will be.

A function that is one-to-one is any function that passes the horizontal and vertical line test which means it is any function that has an inverse. Passing a horizontal line test on a function is the same thing as passing a vertical line test on its inverse function. Graphically when a function is graphed its inverse will be symmetrical to line y=x.

I had some trouble in trying to figure out an answer to a math problem we got in our homework pg 44 number 35 & 36. I am not really sure whether there are different rules when solving an exponential function that has addition on it.